Radiation and the “Inverse-Square” Law
If you have done the FARLabs Nuclear → Turntable experiment, you would know that radiation comes in many forms, including alpha, beta and gamma radiation. BUT did you know that regardless of the type, ALL kinds of radiation are emitted from the source in the same way?
Each little piece of radiation (alpha particle, beta particle or gamma ray) is emitted from the source in a RANDOM direction. It then travels in more or less a straight line.
Imagine two gamma-rays emitted from the same place, but in slightly different directions. As they move away from the source, they get further and further away from EACH OTHER. They are spreading out.
You might like to try this with people in your class room. Stand next to each other then all start walking in slightly different directions, but all walking in your own straight line. You will notice that you get further from each other as you walk.
The separation between two people (or two radiation particles) increases as you move from the place where you started. Increase the distance from the starting point and the separation between particles increases.
Now if we think about the Geiger detector which counts the intensity of the radiation, as we get further from the source, the particles get further and further apart. This means less of them enter the detector together. This is why the counts at the detector decrease as it gets further from the source. Each individual particle is just as “powerful” – they don’t slow down much at all … but less of them enter the detector together.
Here are some examples of this!
Here, a nuclear test sends damaging particles in all directions. A single particle will do just as much damage 20 kilometres away as it will 2 kilometres away. But if the target is closer, A LOT more particles will hit it!
Below is a picture of water being sprayed from a hand-held pump. Water droplets sprayed from the nozzle come out in many directions. If you are very close to the spray, you get very wet. Further away, you just get a little damp!
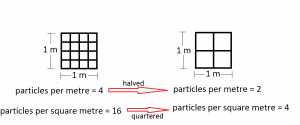
If the number of particles per metre is halved, the number of particles per square metre is quartered.
The “inverse-square” law
If the distance from the source doubles:
- the separation between particles doubles
- the number of particles per metre is halved.
So the number of particles per square metre is quartered.
So the number of particles entering the detector is quartered if the detector is twice as far away! This is what you should have seen in the experiment.
What does “inverse-square” mean – a more advanced explanation
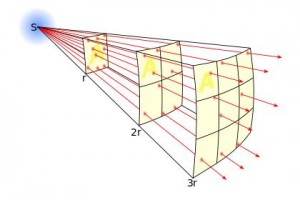
The inverse-square law. The same number of particles passing through an increasing area means the particles per square metre decreases with distance.
In the diagram to the left, as the distance from the source increases, the same number of particles (9 – count them!) are passing by. But the area covered by the 9 particles is increasing as they spread out, at a rate equal to the distance squared. This means double the distance and you double × double = quadruple the area (for example, going from “r” to “2 r” in the picture). So, the number of particles per square metre (which is actually what the detector counts!) is decreasing at a rate equal to the distance squared. This is what “inverse-square” means.
At distance r we have 9 particles spread over 1 square metre; 9⁄1 = 9 particles per square metre. At distance 2 × r we have 9 particles spread out over 4 square metres; 9⁄4 = 2.25 particles per square metre and at distance 3 × r we have 9 particles spread out over 9 square metres; 9⁄9 = 1 particle per square metre.