Virtual Lab - Magnetic Induction
The purpose of this exercise is to observe the relationship between the magnitude of the induced EMF and the applied magnetic field
At the end of this exercise you will have:
• Used appropriate methods for measuring the induced voltage as a function of current, frequency, and angle.
• Plotted correctly drawn graphs and determined the required quantities.
Introduction
A magnetic field, which varies with time, is generated by passing a current through a short coil of wire (for this experiment, two short coils pushed together with a small gap between them). A “search coil” is placed on the axis in the centre of the two coils. Since the magnetic field is varying, an EMF is induced in the search coil. Figure 1.
 Experimental setup, showing the large coils, the search coil, signal generator, and the oscilloscope.
Experimental setup, showing the large coils, the search coil, signal generator, and the oscilloscope. For this experiment you will vary the current, the frequency of generated signal, and the angle of the search coil and determine the induced voltage. Varying these three variables you will confirm the relationship between
εo and Io
εo and ω
εo and θ Equation 3
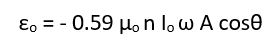 where ω is equal to 2πf
where ω is equal to 2πf
μo = permeability constant = 4π × 10-7 Hm-1
n = number of turns/unit length = 37,777 turns/m for each of the large coils provided
I = current in the coil in Amperes (the same in both large coils)
ω = is directly proportional to the frequency of the input signal f (Hz)
A = cross-sectional area of the search coil 9.5 x 10-5m2
θ = the angle between the large coils and the search coils
 |
Select the parameters of the experiment, default is 1 mA, 100 Hz, 0o
Current (mA) Frequency (Hz) Angle (θ o)
Measurments Current Current is mA Current Frequency is Hz Current Angle is o Induced Voltage is μV |
|---|
The experimental setup
| Measurment | |||
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 |




